안녕하세요. MANVSCLOUD 김수현입니다.
AWS에서 출시한 Amazon Linux 2023에서는 SSH-RSA 알고리즘이 비활성화되어 RSA 공개키를 이용한 SSH 접근에 대한 기본 설정이 비활성화로 변경되었습니다. 이러한 변화를 맞이하여 “SSH-RSA 비활성화로 알아보는 암호화 알고리즘”이라는 제목으로 글을 작성하려 합니다.
가볍게 암호학의 역사로 시작하여 RSA와 Ed25519 등 현대 암호화 알고리즘에 대한 설명으로 독자들이 암호화 기술에 대한 이해에 조금이나마 도움되길 바랍니다.
시작하기 전에 오늘 포스팅은 격식체를 버리고 작성하려 합니다.
🎭
그럼 시작하겠다.😏
Cryptography
현재 보안을 전문적으로 담당하고 있지는 않지만 암호학은 글쓴이가 대학 시절에 가장 관심을 가졌던 과목 중 하나다.
암호학은 인류 역사와 함께 발전해 온 중요하고 재밌는 기술 중 하나로 아주 먼 옛날부터 암호는 쓰여지고 있었는데 역사상 가장 오래된 암호라 불리는 ‘스키테일’ 암호가 있다.
스키테일 암호는 집에서 하나 정도 굴러다니고 있는 모나미 볼펜으로도 실습을 해볼 수 있는 간단한 암호 방식인데 굴러다니는 모나미 볼펜을 발견하지 못했으니 애플 펜슬을 사용해보도록 하겠다.
위 영상에서 볼 수 있듯 애플 펜슬에 종이를 감아 “HELLO MANVSCLOUD” 라고 작성했다.
이후 종이를 펼치게 되면 아래와 같이 암호화된 문자를 볼 수 있다.

“HELLO MANVSCLOUD”가 “OSD LVU LNO EAL HMC”로 변경되었다.
이때 애플 펜슬이 아니라 크기가 다른 각목이나 나무젓가락에 종이를 다시 감으면 어떻게 될까? 당연히 복호화가 되지 않는다.
즉, 여기서 애플 펜슬은 키 역할을 하게 되고 애플 펜슬과 크기가 다른 도구를 사용하면 암호화된 메시지를 복호화할 수 없다는 것을 알 수 있다.
최초의 암호 스키테일을 통해 암호의 시작을 배웠다. 이를 통해 조금이나마 흥미가 생겼길 바란다. 스키테일 외에 다른 고대 암호가 궁금하다면 따로 찾아보길 바란다. 대표적으로 시저 암호, 니힐리스트 암호, ADFGVX 암호 등이 존재한다.
암호학은 시간이 흐르면서 점차 발전하였고 에니그마 암호기가 그 발전의 정점 중 하나로 여겨지는데 에니그마는 2차 세계대전 당시 나치로부터 개발된 암호화 기계로 많은 희생자를 만들어낸 죽음의 암호이기도 하다. 에니그마 암호에 대한 내용까지 이 글에 담아내기에는 내용이 산으로 갈 수도 있으니 한 편의 영화로 감상해보는 것을 추천한다.

‘이미테이션 게임’은 ‘에니그마’ 암호를 해독하는데 성공하며 이로인해 전쟁의 흐름을 바꾸는데 기여한 영국의 수학자 앨런 튜링의 삶을 그린 영화로 암호학에 관심이 있다면 꼭 보길 바란다.
암호학은 이러한 역사를 거치며 현대의 암호화 알고리즘으로 발전해왔다. RSA와 Ed25519 등의 현대 암호화 알고리즘은 인터넷과 기술 발전에 따른 정보 보호의 필요성에 의해 개발되었고 이러한 암호화 알고리즘은 데이터를 안전하게 보호하고 통신의 기밀성과 무결성을 유지하기 위해 널리 사용되고 있다.
RSA
암호학의 역사를 간략하게 살펴봤으니 이제 현대 암호화 알고리즘 중 하나인 RSA에 대해 알아보려고 한다. 암호학을 배우기 위해 우리는 수학적 배경을 빼놓을 수 없기때문에 혹시라도 수학 울렁증이 있다면 미리 마음의 준비를 하기 바란다.
25*33=? 라는 문제를 보면 2*2*2*2*2*3*3*3=864라는 답을 쉽게 얻을 수 있다. 하지만 864만 알고 있다면 25*33이라는 답을 빠르게 내놓을 수 있을까? 어렵다.
(N = P * Q로 P와 Q를 이용해 N을 얻기 쉬운 반면, N을 이용해 P와 Q를 찾기 어렵습니다).
RSA는 이러한 합성수(소수가 아닌 수) 의 소인수 분해의 어려움을 이용한다.

p,q : 비밀, n : 공개, Φ : 비밀, e : 공개, d : 비밀
드디어 Alice와 Bob이 등장할 때다.
(앨리스와 밥은 암호학을 배울 때 흔하게 볼 수 있는 이름인데 그 외에도 이브, 맬로리 등이 존재한다. 앨리스와 밥은 여기서 송신자와 수신자로 보면 된다.)
앨리스와 밥은 각각 공개키와 개인키를 하나씩 가지고 있다.
앨리스는 암호화를 할 때 밥의 공개키를 사용하고, 밥은 자신의 개인키로 복호화하게 된다. 따라서 앨리스가 암호문을 만들어서 밥에게 보낼 때는 밥의 키가 필요하게 되는데 위 RSA 암호 방식 이미지는 밥이 키를 만들어 나가는 과정이라고 볼 수 있다.
5) 과정을 마친 밥은 앨리스에게 e와 n 값을 전달해주고 앨리스는 전달 받은 값을 이용하여 암호화를 할 수 있게된다. 이후 앨리스가 c를 밥에게 보내면 밥은 복호화를 진행한다.
간단하게 Python을 이용하여 RSA 암호화 및 복호화 테스트를 진행해보자.
pip install pycrypto
import random
from Crypto.Util import number
# 소수 p, q를 임의로 선택한다.
p = number.getPrime(1024) # 1024비트 소수
q = number.getPrime(1024) # 1024비트 소수
# N = p * q를 계산한다.
N = p * q
# 오일러 피 함수 Φ(N) = (p-1) * (q-1)를 계산한다.
phi = (p - 1) * (q - 1)
# 공개키 e를 선택한다.
e = 65537
# 다음 조건을 만족하는 개인키 d를 찾는다: (d * e) % Φ(N) = 1
def extended_gcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, x, y = extended_gcd(b % a, a)
return (g, y - (b // a) * x, x)
def mod_inverse(e, phi):
g, x, _ = extended_gcd(e, phi)
if g != 1:
raise Exception("Modular inverse does not exist")
else:
return x % phi
d = mod_inverse(e, phi)
print("Public key (N, e):", (N, e))
print("Private key (N, d):", (N, d))
위 코드는 소수 p, q를 임의로 선택하고, N과 Φ(N)을 계산한 다음, 공개키 e와 개인키 d를 찾아낸다. 아래는 해당 코드를 실행한 결과다.
[root@manvscloud-rsa-pub-kr1 rsa]# python rsa.py Public key (N, e): (27747037819168589670776652666542409321896693698152120734122122563373641022283636067628702081283132225913323238324167213382083559745114980462155495150433321747165116522870896401298003536041275373620597739881114680531282959450539488951414424006509708207627810910385844062091399672482246529383646714566612231321166646601476729844338984924829052224060835042872399943731583214734121114298231944741062167975015603381549215648535923732390831602782260839468027372973819542910735526354706525869942385438107714257584839134281373189010127532918713622103597356039092402593221717411978185319683188067000290171312215562537586767633, 65537) Private key (N, d): (27747037819168589670776652666542409321896693698152120734122122563373641022283636067628702081283132225913323238324167213382083559745114980462155495150433321747165116522870896401298003536041275373620597739881114680531282959450539488951414424006509708207627810910385844062091399672482246529383646714566612231321166646601476729844338984924829052224060835042872399943731583214734121114298231944741062167975015603381549215648535923732390831602782260839468027372973819542910735526354706525869942385438107714257584839134281373189010127532918713622103597356039092402593221717411978185319683188067000290171312215562537586767633, 21028424773829523960024639282265413220012588043392580261873103490816515896284291868821923111725752039255122123397237242386153260683588977975713553155190537017840258288569078268148820355342753944443411333207427925486790088499464353529133948938085725426193724343455515249034219432272582214953796557961067737388698480489620655231384478763210598370338430992204001461313134059445854033126417267356707308500451307467483096602236531535647299658267018242390004042251935585286901805780559761936791230021059283632334258484293091812839408731080491608905149845447655842143728855538529382438225207880855787429510627231591317385153)
이제 이를 사용하여 메시지를 암호화하고 복호화 하는 과정을 구현해보자.
import random
from Crypto.Util import number
# 소수 p, q를 임의로 선택한다.
p = number.getPrime(1024) # 1024비트 소수
q = number.getPrime(1024) # 1024비트 소수
# N = p * q를 계산한다.
N = p * q
# 오일러 피 함수 Φ(N) = (p-1) * (q-1)를 계산한다.
phi = (p - 1) * (q - 1)
# 공개키 e를 선택한다.
e = 65537
# 다음 조건을 만족하는 개인키 d를 찾는다: (d * e) % Φ(N) = 1
def extended_gcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, x, y = extended_gcd(b % a, a)
return (g, y - (b // a) * x, x)
def mod_inverse(e, phi):
g, x, _ = extended_gcd(e, phi)
if g != 1:
raise Exception("Modular inverse does not exist")
else:
return x % phi
d = mod_inverse(e, phi)
print("Public key (N, e):", (N, e))
print("Private key (N, d):", (N, d))
def encrypt_rsa(message, public_key):
N, e = public_key
message_int = int.from_bytes(message.encode(), byteorder='big')
encrypted_int = pow(message_int, e, N)
return encrypted_int.to_bytes((encrypted_int.bit_length() + 7) // 8, byteorder='big')
def decrypt_rsa(encrypted_message, private_key):
N, d = private_key
encrypted_int = int.from_bytes(encrypted_message, byteorder='big')
decrypted_int = pow(encrypted_int, d, N)
return decrypted_int.to_bytes((decrypted_int.bit_length() + 7) // 8, byteorder='big').decode()
# 메시지 정의
message = "Hello, MANVSCLOUD!"
# 암호화
encrypted_message = encrypt_rsa(message, (N, e))
print("Encrypted message:", encrypted_message)
# 복호화
decrypted_message = decrypt_rsa(encrypted_message, (N, d))
print("Decrypted message:", decrypted_message)
encrypt_rsa 함수는 메시지를 정수 형태로 변환한 다음, 공개키(N, e)를 사용하여 암호화된 정수를 계산한다. 이 정수를 다시 바이트로 변환하여 암호화된 메시지를 반환하게 된다.
decrypt_rsa 함수 부분은 암호화된 메시지를 정수 형태로 변환한 다음 개인키(N, d)를 사용하여 복호화된 정수를 계산하고 해당 정수를 다시 바이트로 변환하여 복호화된 메시지를 반환하게 된다.
[root@manvscloud-rsa-pub-kr1 rsa]# python rsa-deep.py Public key (N, e): (25877219463692493414976548387299436809888149433475619052951394961913099193597879724049524963715925846084342752019375664192019871895122430969045682762736995714133503316804268326759852341548507789095005113325181576802425807803187319912388337701067350248297581602479500813719623318429389045256905808816048428404922552276002597709501130061122700109812482842258353518342677582788458587989599549248237049370730483618580002913957156195767479295157497523841229885175331837514314225758740509208580588348733730637647096111049390604779574628860240907400080209011675159993700786649903800928551293299820788454056337806242045117629, 65537) Private key (N, d): (25877219463692493414976548387299436809888149433475619052951394961913099193597879724049524963715925846084342752019375664192019871895122430969045682762736995714133503316804268326759852341548507789095005113325181576802425807803187319912388337701067350248297581602479500813719623318429389045256905808816048428404922552276002597709501130061122700109812482842258353518342677582788458587989599549248237049370730483618580002913957156195767479295157497523841229885175331837514314225758740509208580588348733730637647096111049390604779574628860240907400080209011675159993700786649903800928551293299820788454056337806242045117629, 5650684159252075518588421562943714850943883707561676370093037723727640303333678025098383382756894804206982759725792836569449263571586998330683625524780340047072105314048337336531428763292501868711393841292654127372621812647381078402523604999312981207613816474862812398265735833346704710723279659275927629566477584772007582062653282635747861870542601372349119462841690123454939639075208751704882160739211658028652198076153187894798541271848841946077547483316781117340800973423428662785006024806934891151547468627239372514791949702675953288720169309822134940244734304339906950159066375724080307645806723578611651492101) Encrypted message: b'\xa2\xfb\x02R\xf7\x8e\xcb\x94\xec&\xbd\xfc\x16\xf8\x9c\x9d62\xc8K\xbfk\x80\xca\x8d3\xc3_B\x84(\xf7\xfb\xab\xa0\xd2 \x91Y\xb95\x15WQ\xefR\x85R\x88\t\xd4\x0e\x93\x91\x81q\xfc4L\xeb\xbb\xd7\xd0\x15\xe5\xc2\xaa\x8d\xa6\xfc\x91\x8b\xf0>9\x1a\xa8\xfe&\xdf`\xb0\xf1\x8fi\x1cV\xfd!\xf1\x818(^\xabUh\x10K\x8d\xcdn\x9b\xeb\x94u\t\xf6\x1d\x8fV^\xfc\xeb\xber\xe30\xcb\xb8\xb69\xf1\\\x86\xf3\xfeYGw\x1e\xf6\xce8\xca4!\xc3\x1e\xaf\xe1\xea<B\xd0%q\x91\x83Q\xc2S\x97$\xe5j\xe2te\xcf\xc5\x10\x15\xa33\xd0\r\xd0;\x07\xddc\xf0H9\xb3B\xf1\xa2F\xd1$\xc3Tk\xe7\x97\xf8\x9d*\xa5\x92\x90\xd2\xe0\x81W\x9c\xe1\xf3+\xb5j\xa93-\xf2\x8b\xf1\x8f\x8b\x99\x84\xc0\xab\x9b\x12\xcc\xba&\x818H!\xa6\xf5.\xea\xd2\x9b-=\xbaG\x05\xd2P\xe8V\xec\x14\xc6\xc4[\xd1,\xf04\xf0\x899\xdd\x0c-b\xdb' Decrypted message: Hello, MANVSCLOUD!
메시지 “Hello, MANVSCLOUD!”를 암호화 하고 복호화 하는 과정을 수행보았다.
그렇다면 RSA는 어떻게 사용되고 있을까? RSA는 최초의 전자 서명이 가능한 알고리즘으로 공개키를 이용하는 대표적인 암호화 방식이다. 흔히 알고 있는 SSH 프로토콜, SSL/TLS 프로토콜에서도 사용되고 있다.
Linux에서 SSH 서버의 설정 파일인 /etc/ssh/sshd_config 파일을 살펴보면 SSH 서버가 사용할 RSA 호스트 키 파일의 위치가 지정된 것을 알 수 있다.
HostKey /etc/ssh/ssh_host_rsa_key #HostKey /etc/ssh/ssh_host_dsa_key HostKey /etc/ssh/ssh_host_ecdsa_key HostKey /etc/ssh/ssh_host_ed25519_key
해당 경로에서 다양한 키 파일을 확인할 수 있는데 대표적인 예시로 /etc/ssh/ssh_host_rsa_key 파일은 호스트의 RSA 개인키를 포함하며 해당 공개키는 /etc/ssh/ssh_host_rsa_key.pub 파일에 저장된다.
[root@manvscloud-rsa-pub-kr1 manvscloud]# ll /etc/ssh total 608 -rw-r--r--. 1 root root 581843 Aug 9 2019 moduli -rw-r--r--. 1 root root 2276 Aug 9 2019 ssh_config -rw------- 1 root root 3937 Jun 22 2022 sshd_config -rw-------. 1 root root 3906 Aug 31 2020 sshd_config_org -rw-r-----. 1 root ssh_keys 227 Aug 31 2020 ssh_host_ecdsa_key -rw-r--r--. 1 root root 162 Aug 31 2020 ssh_host_ecdsa_key.pub -rw-r-----. 1 root ssh_keys 387 Aug 31 2020 ssh_host_ed25519_key -rw-r--r--. 1 root root 82 Aug 31 2020 ssh_host_ed25519_key.pub -rw-r-----. 1 root ssh_keys 1675 Aug 31 2020 ssh_host_rsa_key -rw-r--r--. 1 root root 382 Aug 31 2020 ssh_host_rsa_key.pub
우리는 AWS의 [키 페어]에서 만들어진 키를 이용하여 EC2를 생성한다.
여기서 발급된 .pem 키는 개인키일까? 공개키일까?
그리고 SSH 접속 시 공개키 인증을 사용하여 접속할 경우 아래와 같이 숨긴 폴더 아래 authorized_keys 파일이 있다. 이 파일은 개인키일까? 공개키일까?
[root@manvscloud-rsa-pub-kr1 manvscloud]# tree .ssh .ssh └── authorized_keys
.pem 파일은 개인키다. 이에 대응하는 공개키가 서버 내에 저장되어있어야 하는데 이 공개키가 저장된 파일이 바로 .ssh/authorized_keys의 정체다.
//sshd_config 참고 # The default is to check both .ssh/authorized_keys and .ssh/authorized_keys2 # but this is overridden so installations will only check .ssh/authorized_keys AuthorizedKeysFile .ssh/authorized_keys
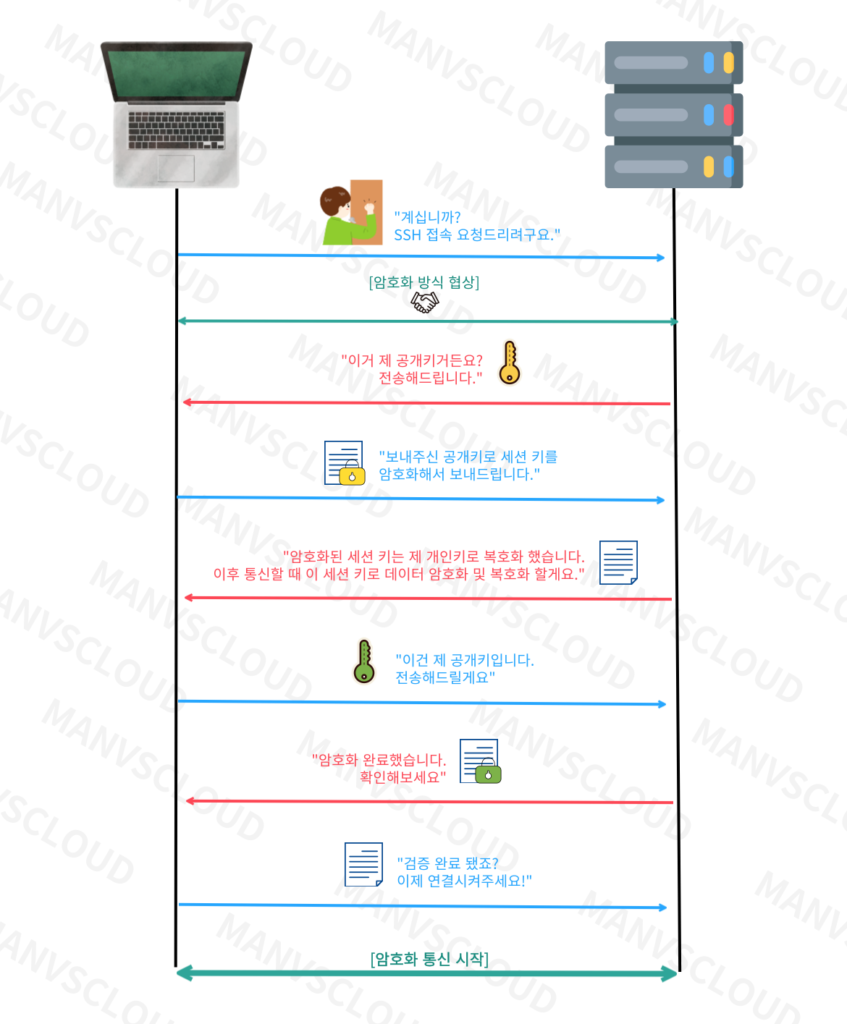
위 이미지는 SSH 접속 과정을 보여준다. 지금까지 알아본 RSA 암호화 방식과 공개키-개인키 구조를 고려하며 이들이 어떻게 상호작용하여 연결이 이루어지는지 다시 생각해보기 바란다.
Good-Bye RSA
지원 중단 임박 알림
===========================
OpenSSH는 기본적으로 ssh-rsa 서명 체계를 비활성화합니다.

Amazon Linux 2023(AL2023)에는 레거시 ssh-rsa호스트 키 알고리즘을 비활성화하고 축소된 호스트 키 세트를 생성하는 기본 구성이 포함되어 있습니다.
OpenSSH 8.7부터 기본적으로 ssh-rsa 서명 체계를 비활성화한다는 내용이 포함되어있다.
OpenSSH 8.7이 반영된 Amazon Linux 2023 AMI를 사용하는 EC2 인스턴스에서 기존 RSA 키로는 SSH 접근을 할 수 없어 이에 대한 사용자들의 질문이 하나둘씩 나오고 있다.
이제는 RSA를 보내줘야할 때인가? 그렇다면 왜 이제 RSA를 보내줘야 하는가?
OpenSSH가 최신 버전에서 RSA를 비활성화하는 주요 원인은 무엇일까? 이유는 간단하다. 더 안전하고 훌륭한 대안이 존재하기 때문이다.
RSA의 키 길이는 길다. 물론 길어질수록 보안이 강화되지만 길어진만큼 연산이 느려질 수 밖에 없다. 물론 현대의 컴퓨터는 빠르게 발전하고 있기때문에 길어진 키 길이로 인한 성능 저하를 크게 걱정하지 않을 수 도 있다. 그러나 반대로 생각해보면 공격자의 컴퓨터도 빠르게 발전하여 RSA 키를 해독하는데 필요한 시간이 크게 증가하지 않는다. 이는 보안성이 점차 약화되는 것을 의미하기도 한다.
또한 RSA 알고리즘이 수학적으로 안전하다고 알려져 있지만 알려진 취약점이 존재한다. 이러한 취약점은 시간이 지남에 따라 발견되고 개선되지만 결국 완전히 안전한 암호화 알고리즘은 아닌 것이다.
양자 컴퓨터의 발전으로 인해 RSA와 같은 전통적인 암호화 알고리즘은 더욱 위협을 받을 수 밖에 없는데 양자 컴퓨터는 RSA와 같은 암호화 체계를 빠르게 해독할 수 있는 능력이 있어 RSA 알고리즘을 지속적으로 사용하는 것은 미래의 보안에 위험 요소가 될 수 있다고 예상된다.
이러한 RSA의 문제점으로부터 더 훌륭한 대안으로 Ed25519나 ECDSA와 같은 공개키 암호화 체계가 있다. RSA가 소인수분해의 어려움을 사용했다면 Ed25519나 ECDSA는 타원 곡선 암호화로 주로 이산 로그 문제의 어려움을 이용한 케이스다.
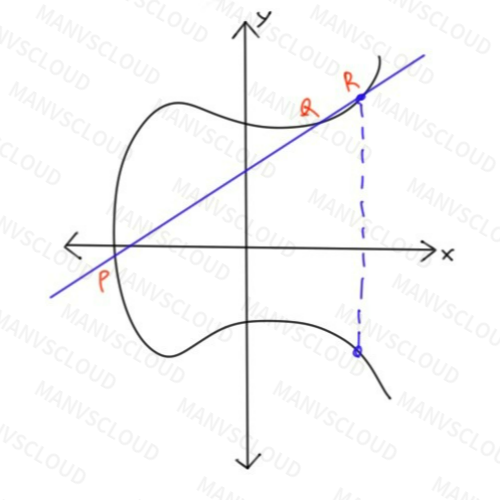
타원 곡선에서 이산 로그 문제는 해결하기 매우 어려운 것으로 알려져 있으며 이로 인해 공격자가 키를 추측하거나 무력화하는 것이 현실적으로 불가능하다.
추가로 타원 곡선 기반의 알고리즘은 RSA와 같은 전통적인 공개키 암호화 방식보다 더 강력한 보안성을 제공하지만 RSA보다 짧은 키 길이를 사용한다.
이러한 이유로 인해 OpenSSH는 더 안전한 대안인 Ed25519나 ECDSA와 같은 타원 곡선 기반의 공개키 암호화 체계를 사용하여 인증을 처리하는 것을 권장하고 있다.
Elliptic Curve Cryptography(ECC) 즉, 타원 곡선 암호를 이용한다면 보안성은 높이고 키 길이는 짧게하여 높은 수준의 보안을 가질 수 있게 되는 것이다.
예를 들어 3072비트 RSA 키는 대략 128비트의 보안 수준을 제공하는 반면 256비트의 ECDSA 키 또는 Ed25519 키는 같은 수준의 보안을 제공한다. 이는 타원 곡선 암호화가 더 효율적으로 공간을 활용하고 키 관리를 간소화하는 동시에 높은 보안성을 유지한다는 것을 의미한다.
짧은 키 길이 덕분에 저장 공간과 전송 대역폭이 절약되며 전력 소모도 줄일 수 있는데 특히 모바일 기기나 IoT 기기와 같은 제한된 리소스를 가진 환경에서 중요한 이점이 된다.
대표적으로 ECDSA와 Ed25519 암호화 알고리즘은 블록체인 기술에서도 사용되고 있다.
Ed25519
Amazon Linux 2023 AMI를 이용하여 인스턴스를 생성해보면 /etc/ssh 경로 내에 파일들이 기존 Amazon Linux 2와는 달라진 것을 확인할 수 있다. sshd_config 내용도 변경되었지만 무엇보다 해당 디렉토리에서 이제는 ssh_host_rsa_key와 ssh_host_rsa_key.pub 두 키 파일을 찾을 수 없다.
[root@ip-10-0-11-33 ssh]# ll total 592 -rw-r--r--. 1 root root 578094 Jan 30 02:45 moduli -rw-r--r--. 1 root root 1921 Jan 30 02:45 ssh_config drwxr-xr-x. 2 root root 28 Apr 4 18:13 ssh_config.d -rw-r-----. 1 root ssh_keys 557 Apr 10 00:00 ssh_host_ecdsa_key -rw-r--r--. 1 root root 212 Apr 10 00:00 ssh_host_ecdsa_key.pub -rw-r-----. 1 root ssh_keys 452 Apr 10 00:00 ssh_host_ed25519_key -rw-r--r--. 1 root root 132 Apr 10 00:00 ssh_host_ed25519_key.pub -rw-------. 1 root root 3746 Apr 10 00:00 sshd_config drwx------. 2 root root 28 Apr 4 18:13 sshd_config.d
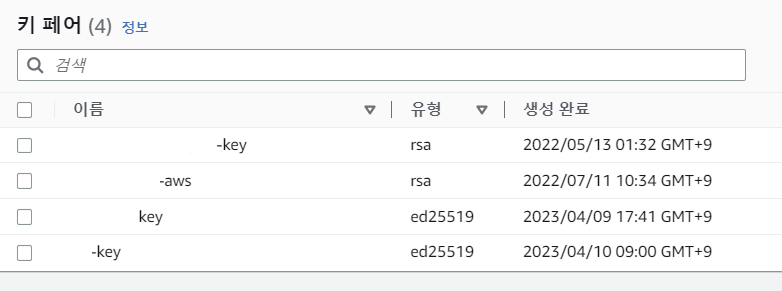
인스턴스 생성 시 기존 RSA 키가 아니라 ed25519 유형의 키로 새로 만들어서 생성해주어야한다.
키 페어 생성 시에 유형을 직접 선택할 수 있으니 참고하자.
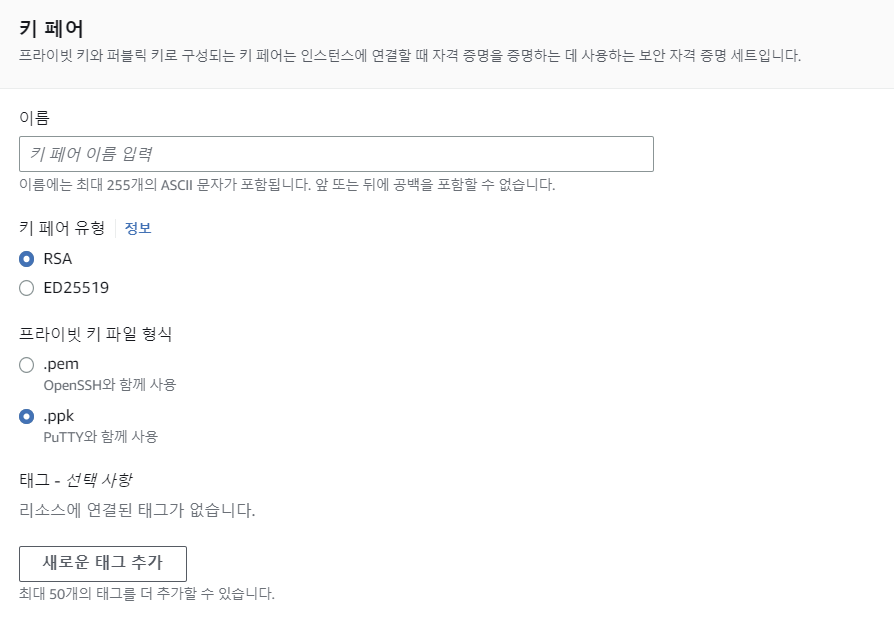
ssh-keygen을 이용하여 RSA 알고리즘 키를 만들었던 것처럼 Ed25519 키 역시 ssh-keygen으로 생성할 수 있다.
사용자 생성 후 ssh-keygen로 Ed25519 유형 키를 생성하고 생성된 키를 이용해서 SSH 접속을 해볼 수 있다.
[root@ip-10-0-11-33 root]# useradd manvscloud [root@ip-10-0-11-33 root]# cd /home/manvscloud/ [root@ip-10-0-11-33 manvscloud]# mkdir .ssh [root@ip-10-0-11-33 manvscloud]# chmod 700 .ssh [root@ip-10-0-11-33 manvscloud]# touch .ssh/authorized_keys [root@ip-10-0-11-33 manvscloud]# chmod 600 .ssh/authorized_keys [root@ip-10-0-11-33 manvscloud]# chown -R manvscloud:manvscloud .ssh // 위 과정은 사용자 생성 후 권한을 주는 부분이고 아래 과정이 Ed25519 유형의 키를 생성하는 부분이다. [root@ip-10-0-11-33 manvscloud]# ssh-keygen -t ed25519 -f ed25519_key Generating public/private ed25519 key pair. Enter passphrase (empty for no passphrase): Enter same passphrase again: Your identification has been saved in ed25519_key Your public key has been saved in ed25519_key.pub The key fingerprint is: SHA256:zucqCpYnVH11E+caNAOQhiSIzXiwXXWc/FZSVTn5f7I root@ip-10-0-11-33.ap-northeast-2.compute.internal The key's randomart image is: +--[ED25519 256]--+ |.* .ooo+o+ooOoo.+| |oo=. o..*..o.* + | |... . .... o. . o| | . . o o .| | . S. . .| | . . o . o| | = . o . o.| | . + . o E | | .. .... | +----[SHA256]-----+ [root@ip-10-0-11-33 manvscloud]# ll total 8 -rw-------. 1 root root 452 Apr 10 01:55 ed25519_key -rw-r--r--. 1 root root 132 Apr 10 01:55 ed25519_key.pub [root@ip-10-0-11-33 manvscloud]# cat ed25519_key.pub > .ssh/authorized_keys [root@ip-10-0-11-33 manvscloud]# mv ed25519_key ed25519_key.pem
위 생성된 파일 중 ed25519_key가 개인키, ed25519_key.pub가 공개키다.
ed25519_key.pem 파일을 PC로 다운 받아서 SSH 접속을 진행해보면 접속이 잘 될 것이다.
, #_
~\_ ####_ Amazon Linux 2023
~~ \_#####\
~~ \###|
~~ \#/ ___ https://aws.amazon.com/linux/amazon-linux-2023
~~ V~' '->
~~~ /
~~._. _/
_/ _/
_/m/'
[manvscloud@ip-10-0-11-33 ~]$
물론 여러분들에게 보여주고자 하는 것은 로그인이 됐다는 점이 아니다. RSA키와 Ed25519키의 길이 차이를 보여주고 싶은 것이 핵심이었다.
RSA 키는 ssh-keygen -t rsa -f rsa_key 명령어로 생성할 수 있고 -b 옵션을 추가하여 비트수를 수정할 수 있다. 디폴트 값은 2048인 점을 참고하여 테스트 해보길 바란다.
<RSA Key>
-----BEGIN OPENSSH PRIVATE KEY----- b3BlbnNzaC1rZXktdjEAAAAABG5vbmUAAAAEbm9uZQAAAAAAAAABAAABlwAAAAdzc2gtcn NhAAAAAwEAAQAAAYEAoKMySntvi+iU0pjjxxZEOV13NwdeNyDB8exPWkgoqFadi0FKdA+Q LT6yXSzTHv54qEpApEbe5nl1mnQz8HEUF/+rkLl1Fj1pfp3ncBoBC0q0bU4JUDuumwYjx3 5B47mZOtxNyKHqwDJzUXMLX6TlL7DPqAMP6Lawwx5/wNJnBz6CmoUWHgnVerc5cySouObP PcPM0QAzfCgT1P87GxhOqIkAerWBjyPUp7BE6LqDFDzoJh0Q0EOeLU9GYa0nUcfpyCvAaX QbeWVUyepFGNEwbEKGgzoS1NpTzQ8o9rKsxw9h9XvEgwDnTBxXRZhekERsZV1+x+gf5fzI ehB9kJNfU5KBHieU4KS4VCO7hM5TkSTqVBpMCOU/0gdjOCIyQYO86mlN5tdh13vsvMqivk +Yio1ZBAyXe8UqXd7hzX5jg8QtHLCfo/qChq0EQea3JSs9yha1vGiNEP6pH1GCZjTnevO9 07HfoJ4EQrTbDvpOVQpWgBJFB4U2KpwFEK/uiEFHAAAFqCwXNi8sFzYvAAAAB3NzaC1yc2 EAAAGBAKCjMkp7b4volNKY48cWRDlddzcHXjcgwfHsT1pIKKhWnYtBSnQPkC0+sl0s0x7+ eKhKQKRG3uZ5dZp0M/BxFBf/q5C5dRY9aX6d53AaAQtKtG1OCVA7rpsGI8d+QeO5mTrcTc ih6sAyc1FzC1+k5S+wz6gDD+i2sMMef8DSZwc+gpqFFh4J1Xq3OXMkqLjmzz3DzNEAM3wo AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA xcEaaP017ZddvfTwsYbvQQufm/w48Bm4aqZr5AvgtnduGztImJ/rnT4hMxL0PzV77LWP6K xUlC0/fgXu9jvr8pwLi1+xXkq2xDkFiISWyMY5QLb/HPwst59qtoJJ0yos37pkv456nEXM zJpq5xHQBOcyn1aJcYPlB784dNqn1+xge/l1ZizEI+Z0Nn8/HA6962ocFKc3k6VewxAAAA wAaw28isqZO47CtEHew2S/NsLVMAiQhzonOe3RL8S9hdKzDOLNxpHv8yx29RYqFy4KNJSF rCuibiIPmPJfcmf7VGmDFcKEEC2SgG2Poz8d/eOsQJpY/k4nxn5nUFU08l7u3zvmXA7kF1 OmfRDSXjNqb45LRDYtzTbo6w8qTXOGzJw3odyHsGcW5BBjVxO8ykUkbF1kPDozj9JUwclV sdQBVwhHZYWjZ1tTHJRF/hPKv3NhHHRh+FteodG/MbslwjfgAAAMEAz5HQ5hIe5xy1yOX0 WoeelG5jI5LtlmD7cuPJ+37cn8rZGkXHwPd8MCtbb48tPFit+6i0OOLM/bZmQINd1/KBGo Uo+QTC2gdg5YP4oEfYrgZ+In6vy53DxvtWoOGpVmizPm3GyX/CJqEqpkdrAPrbGpqq9RfI UzBBVLkEYKzV3OTfrg9V2pNtOFRwyFamLuxhPikXmYvI3baFj65ua53k8+UFdemaQHKxVM vPFfjxO1/LtZ1hnj70tQQpYPN+F1X5AAAAwQDGHh0lqdpN45ktcCNafrBKD4E5XmNrn2t/ Xe1+3m8cpFSXkAGSQbdBk99BKECeAte5EybKLk0Arm3emBTFTHUJsjcZhpf2U1Hm2sl1eM 9S+f3n7jRoLyeRiyynM+DSzntibMaJtLxo/yUvtk6t3xD3pJpGuPlOZox97Nx/hu0n2vwS Qa+7cVI1bMzfNCU49zoJxrlwg+NhJMrysor6/zjMF6COMIFcA4sXTc77i0vSwjJnrl6NQx S8gbswC0OdIT8AAAAycm9vdEBpcC0xMC0wLTExLTMzLmFwLW5vcnRoZWFzdC0yLmNvbXB1 dGUuaW50ZXJuYWwB -----END OPENSSH PRIVATE KEY-----
<Ed25519 Key>
-----BEGIN OPENSSH PRIVATE KEY----- b3BlbnNzaC1rZXktdjEAAAAABG5vbmUAAAAEbm9uZQAAAAAAAAABAAAAMwAAAAtzc2gtZW AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA L4G2MSWNzoLKDJrRPZn4AAAAMnJvb3RAaXAtMTAtMC0xMS0zMy5hcC1ub3J0aGVhc3QtMi 5jb21wdXRlLmludGVybmFsAQID -----END OPENSSH PRIVATE KEY-----
위에 보이는 두 테스트용 키 파일을 비교해보면 Ed25519의 키 길이가 매우 짧은 것을 알 수 있다. 그런데 보안면에서 더 뛰어나다고? 가즈아ㅏㅏ! 는.. 안된다. 🙅🏻♂️
기존 시스템 환경에서 호환성 문제가 발생하지 않도록 고려한 후 반영할 필요가 있다.
하지만 알다시피 우리는 미루고 미루다 어느 날 갑자기 ECC 알고리즘 강제화를 눈물과 함께 맞이하게 될 것…😢
Personal Comments
원래 디피-헬만(diffie-hellman)이라던가 모듈러(modular) 등 더 많은 내용을 다루고 싶었지만 전체적인 난이도를 낮추어 누구나 읽기 쉽게 작성하려고 노력했다.
필요한 부분만 최대한 압축하여 소개했기 때문에 더 깊이 있는 암호학의 세계를 탐구하고자 한다면 추가적인 학습을 통해 고통받을 수 있을 것이다.
마지막으로 이 글을 통해 암호화 알고리즘의 기초를 이해하는 데 조금이나마 도움이 되었길 바란다.


1 Comment
감사합니다. 좋은 내용이였어요..